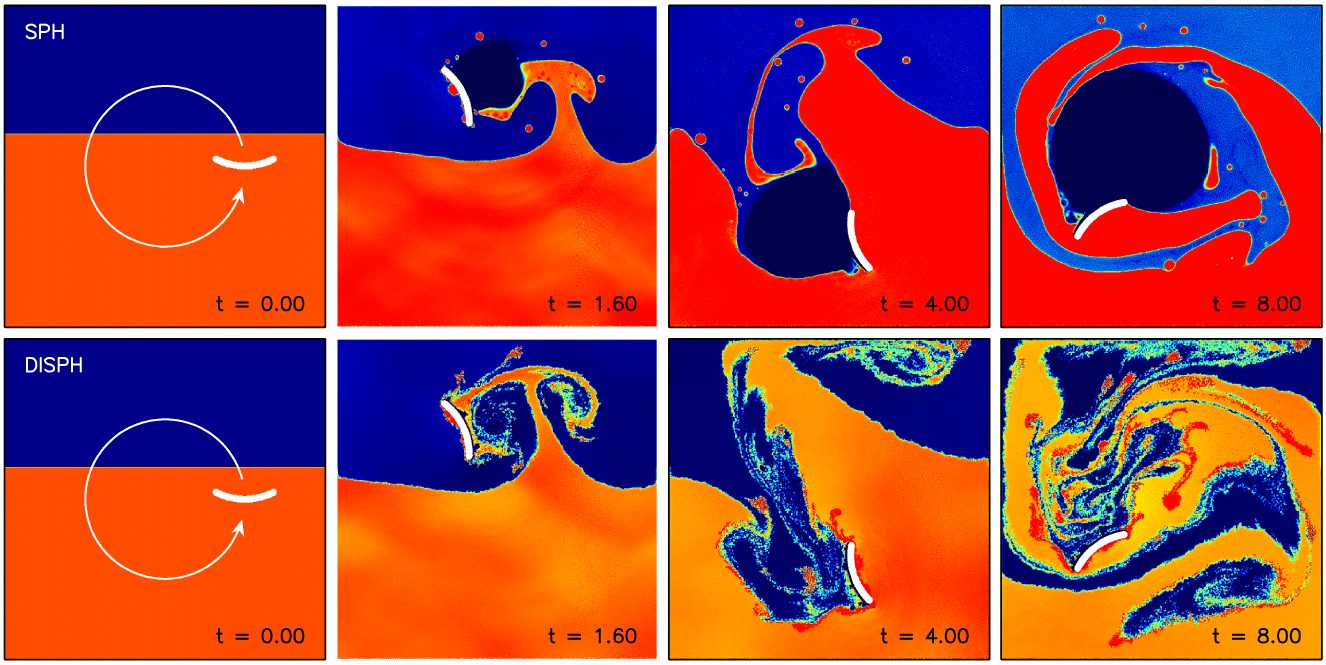
A Density Independent Formulation of Smoothed Particle Hydrodynamics Authors: Takayuki Saitoh & Junichiro Makino (Tokyo Institute of Technology) Link to Astro-ph & ADS Abstract: The standard formulation of the smoothed particle hydrodynamics (SPH) assumes that the local density distribution is differentiable. This assumption is used to derive the spatial derivatives of other quantities. However, this assumption breaks down at the contact discontinuity. At the contact discontinuity, the density of the low-density side is overestimated while that of the high-density side is underestimated. As a result, the pressure of the low (high) density side is over (under) estimated. Thus, unphysical repulsive force appears at the contact discontinuity, resulting in the effective surface tension. This tension suppresses fluid instabilities. In this paper, we present a new formulation of SPH, which does not require the differentiability of density. Instead of the mass density, we adopt the internal energy density (pressure), and its arbitrary function, which are smoothed quantities at the contact discontinuity, as the volume element used for the kernel integration. We call this new formulation density independent SPH (DISPH). It handles the contact discontinuity without numerical problems. 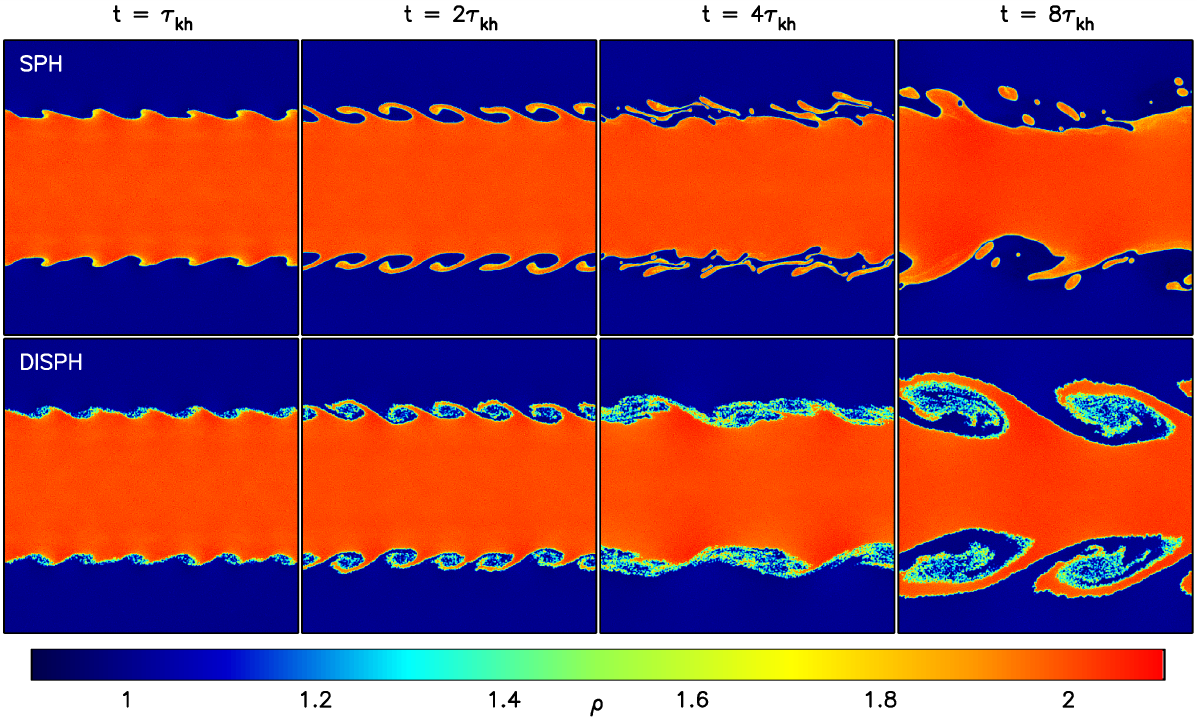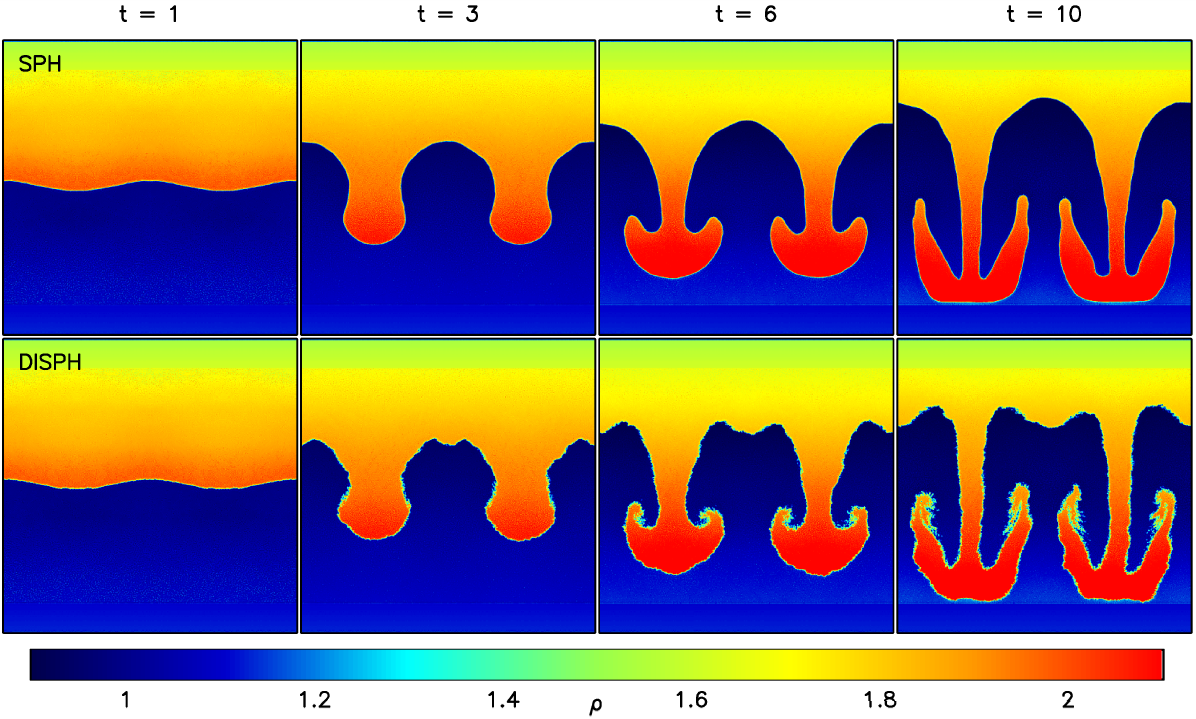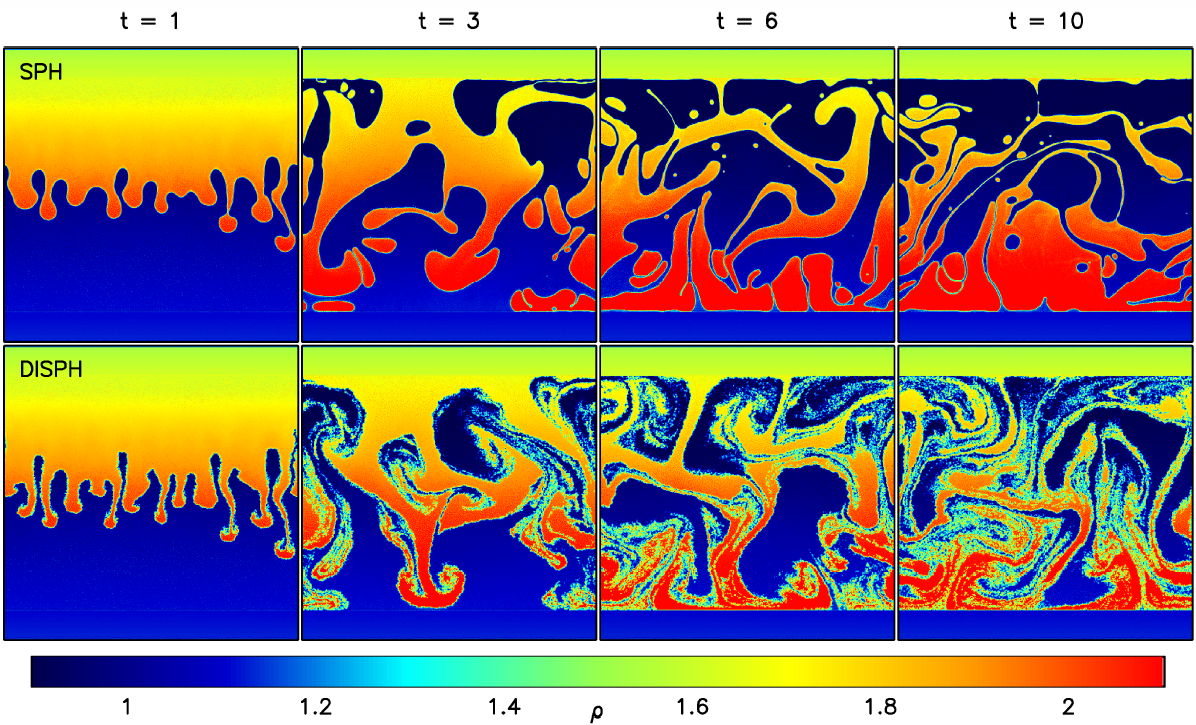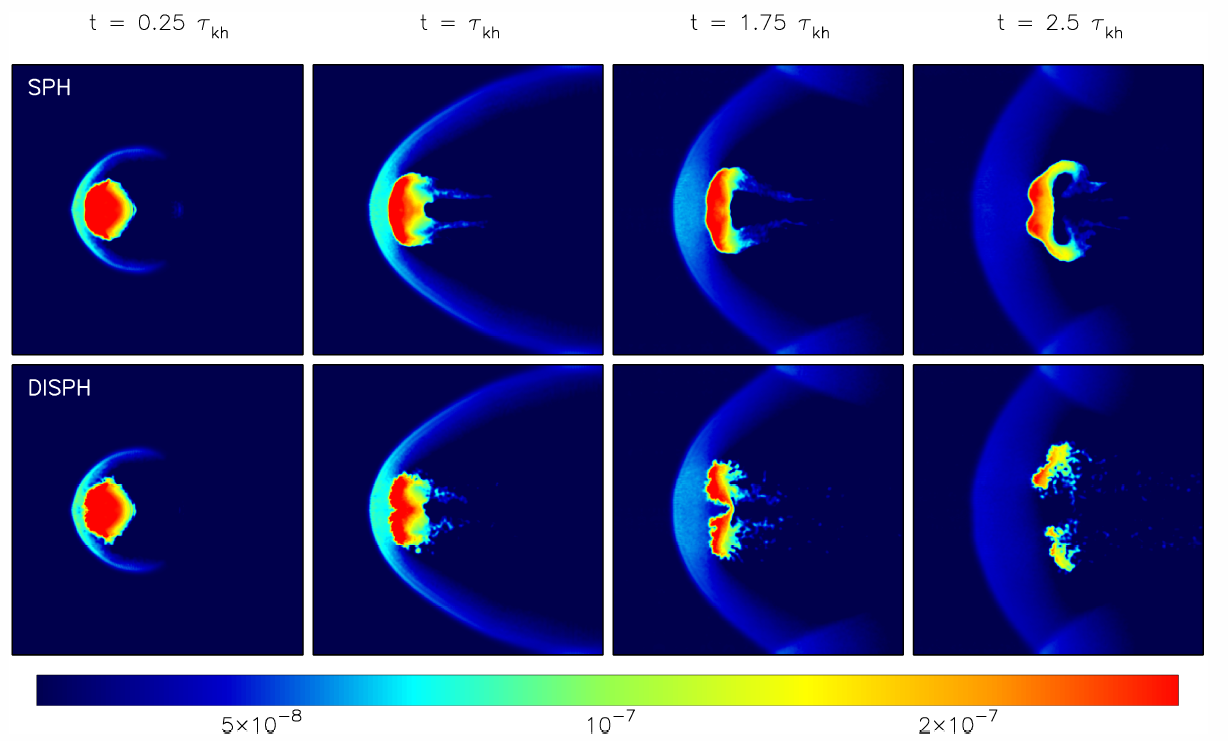The results of standard tests such as the shock tube, Kelvin-Helmholtz and Rayleigh-Taylor instabilities, point like explosion, and blob tests are all very favorable to DISPH. We conclude that DISPH solved most of known difficulties of the standard SPH, without introducing additional numerical diffusion or breaking the exact force symmetry or energy conservation. Our new SPH includes the formulation proposed by Ritchie & Thomas (2001) as a special case. Our formulation can be extended to handle a non-ideal gas easily. The manuscirpt with high-resolution figures is here Old manuscirpt is here Movies

Hydrostatic equilibrium tests Download movie with the standard SPH with the equal mass particles (mp4, 4.6MB) or (ogv, 4.6MB) Download movie with the standard SPH with the equal separation (mp4, 5.1MB) or (ogv, 5.1MB) Download movie with DISPH with the equal mass particles (mp4, 4.3MB) or (ogv, 4.3MB) Download movie with DISPH with the equal separation (mp4, 4.3MB) or (ogv, 4.3MB)

Kelvin-Helmholtz instability tests Download movie with the standard SPH (mp4, 2.3MB) or (ogv, 2.3MB) Download movie with DISPH(mp4, 3.8MB) or (ogv, 3.8MB)

Rayleigh-Taylor instability tests with the single-mode perturbation Download movie with the standard SPH (mp4, 1.3MB) or (ogv, 1.3MB) Download movie with DISPH(mp4, 1.5MB) or (ogv, 1.5MB)

Rayleigh-Taylor instability tests with the multi-mode perturbation Download movie with the standard SPH (mp4, 3.1MB) or (ogv, 3.1MB) Download movie with DISPH(mp4, 6.7MB) or (ogv, 6.7MB)

Blob tests Download movie with the standard SPH (mp4, 0.5MB) or (ogv, 2.0MB) Download movie with DISPH (mp4, 0.5MB) or (ogv, 2.2MB) Download movie (close up) with the standard SPH (mp4, 0.9MB) or (ogv, 3.8MB) Download movie (close up) with our new SPH (mp4, 0.7MB) or (ogv, 3.8MB) Download movie (close up: face-on) with the standard SPH (mp4, 0.8MB) or (ogv, 3.7MB) Download movie (close up: face-on) with our new SPH (mp4, 1.1MB) or (ogv, 3.7MB)

Mixing tests Download movie with the standard SPH (avi, 4.4MB) Download movie with DISPH (avi, 9.0MB)